Topic M

TOPIC M: Recursion

Exercises :

(D1) Arrow.

(S1) Factorial.

(S2) Fibonacci.

(S3) Backtracking

(S4) Fractals.

(X1) Opposite order.

(H1)

(H2)

(T1) Output

D1: Arrow.

Study the : Make the arrow of Topic A S2 by recursion.
Study the recursion with the debugger!!

Hint: Press Ctrl+F7 (Step Over) at LineOfAsterisks()

S1: Factorial.

Calculate a factorial with recursion
see Topic F: S1

S2: Fibonacci.

Calculate the nth Fibonacci number with recursion (see Topic B: H1).

They are defined as a sequence of numbers:

N<1> = 1, N<2> = 1
N<i> = N<i-1> + N<i-2> for i > 2
Count the number of procedures calls (aantal keren dat de recursieve procedure werd aangeroepen).

Hoeveel geheugen is er nodig om de gegevens tijdens de uitvoering te bewaren voor Fib(5), wetend dat variabelen en adressen 4 bytes lang zijn, behalve booleaanse variabelen die maar 1 byte lang zijn.

elke module en procedure heeft een adres nodig voor de allocatierecord, de statische en dynamische band (zie theoriecursus 7.3)
oplossing

S3: Twisting Triangle.

Draw the following picture with recursion

you can find the (n)^th fraction of a line as shown here:

tip: x₁-x₀ or y₁-y₀ can be negative, so it's better use INTEGERs

make sure you can easily change the fraction n and the number of triangles drawn
animate the triangles by drawing them outside-in, then make them disappear inside-out
additional challenge: write the procedure in such a way that it will draw any shape (not just a triangle)
fill with (random?) colors instead of drawing the outline for nice visual appeal
animation

S4: Backtracking.

Gegeven volgende graph:

Maak een procedure die het kortste pad tussen 2 nodes kan berekenen. Zoek dan het kortste pad tussen nodes 1 & 8. Start met deze code.
Los op mbv. backtracking, maar optimaliseer je zoeken door de paden uit te sluiten waarin een node meermaals voorkomt.
oplossing:

S5: Fractals.

Fractals are nice, practical examples of using recursion.
Start with this code.

Look first at this educational website on fractals:

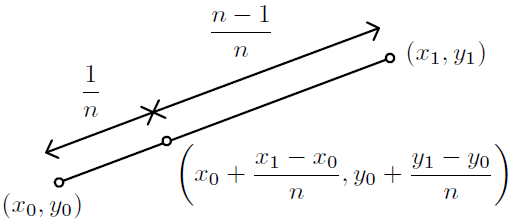
Choose a type of fractal, by pressing Type

Create the fractal iteration by iteration, by pressing the black Play sign.

Draw one of the following fractal figures with recursion (in order of difficulty), also use delays and colors:

The Koch Curve

use the given EquilateralTriangle (tekent een gelijkzijdige driehoek gegeven 2 punten) and the DivideLineIn3 procedure

The Koch Snowflake (uitbreiding van de Koch curve)

use the given EquilateralTriangle (tekent een gelijkzijdige driehoek gegeven 2 punten) and the DivideLineIn3 procedure

detailed explanation

The anti-snowflake

use the given EquilateralTriangle procedure (tekent een gelijkzijdige driehoek gegeven 2 punten)

The Sierpinski Triangle

use the given Triangle and CentralPoint (= Middelpunt) procedure

detailed explanation

Use for Bush One and Bush Two the DivideLineIn3 and RotatePoint procedures.
The Dragon Curve

Elders noemt de curve The Jurassic Park Fractal (de uitleg over het algoritme is hier onnodig ingewikkeld gemaakt, lees het onderstaande)
gebruik de gegeven procedure DrawNextLine en het gegeven type DirectionEn
Gegeven een array van een zekere grootte van DirectionEn, het algoritme ziet er als volgt uit

PROCEDURE VulArrayMetVolgendeIteratie(i: index van het eerstvolgend nog niet ingevuld vakje);
zet een RIGHT op het volgend element (i)
vul de volgende elementen met een lus (teller j), element i+j = de tegengestelde waarde (LEFT <=> RIGHT) van vakje i-j, j dus gaande van 1 tot i-1
volgende iteratie
END
als array gevuld is => teken ze met de DrawNextLine procedure (hoeft niet recursief)

Zo krijg je

iteratie 1: R
iteratie 2: R R L
iteratie 3: R R L R R L L
iteratie 4: R R L R R L L R R R L L R L L

The Hilbert and Stairs curve can be created with the given DivideLineIn3 procedure.
The other are more difficult...

X1: Opposite Order.

Write a procedure that asks a sequence of numbers (terminated by 0), and then writes those numbers in opposite order.
Don't use arrays or pointers ! Use recursion.

H1:

H2:

T1: Output (exam '97)

What is the output of the following program?

Solve it first ON PAPER, then check it on computer.

Remember:

ORD('a') => 97

CHR(97) => 'a'

Hoeveel geheugen is er nodig om de gegevens tijdens de uitvoering te bewaren, wetend dat variabelen en adressen 4 bytes lang zijn, behalve booleaanse variabelen die maar 1 byte lang zijn.

elke module en procedure heeft een adres nodig voor de allocatierecord, de statische en dynamische band (zie theoriecursus 7.3)

MODULE Test1;
FROM IO IMPORT WrLn, WrChar;

PROCEDURE Print(x: CHAR);
    VAR i:CHAR;
BEGIN
    WrChar(x);
    FOR i := 'a' TO x DO
      WrChar('x');
    END;
    WrLn;
    IF x > 'a' THEN
      Print(CHR(ORD(x) - 1));
    END;
    WrChar(x);
    FOR i := 'a' TO x DO
      WrChar('x');
    END;
    WrLn;
END Print;

BEGIN
Print('e');
END Test1.