


TOPIC F: Procedures.
Contents :
 PROCEDURE, open arrays, HIGH().
PROCEDURE, open arrays, HIGH().
Exercises :
D1: SumDivisibleBy.
copy the  to a new file, run it and try to understand it...
to a new file, run it and try to understand it...
- write a procedure that takes 3 cardinals x1, x2 & x3 and
checks
wether
the sum of x1 & x2 is divisible by x3.
- eg: x1 := 10, x2 := 6, x3 := 4 will return TRUE
because 10
+ 6 = 16 is divisible by 4.
- Test this by calling the procedure.







S1: Factorial (faculteit)
- Calculate Cn,p
= n!
/ (n-p)!.p!
- hint: make a
procedure
to calculate the factorial of a given number!
- note that p may
not be
bigger
than n






S2: Search (bis)
Start with your solution of Topic C: S1
and
put
your
search code in a procedure:
- Create a procedure that takes a word and a letter as input, and
that returns the
number
of appearances of the given letter in the word.
- In your main program, do the following 3 times (using your
procedure):
- Ask the user for a word (of maximal 30 characters) and a letter.
- Print the number of appearences of the letter in the word.






S3: Vierkanten & Sterretjes
Gebruik de graph-procedures Line
en Polygon (de definities van deze vind je in wimdows.def of voor de oude graph
gebruikers in graph.def die
in C:/bin/XDS/def/ts staat).
- Maak een procedure die een vierkant tekent met gegeven
middelpunt, de
grootte
en de kleur.
- Line is als volgt gedefinieerd: PROCEDURE
Line(x1, y1, x2, y2, color:CARDINAL);
- Maak een procedure die een jodenster tekent met gegeven
middelpunt,
grootte
(zie S van de tekening) en de kleur.
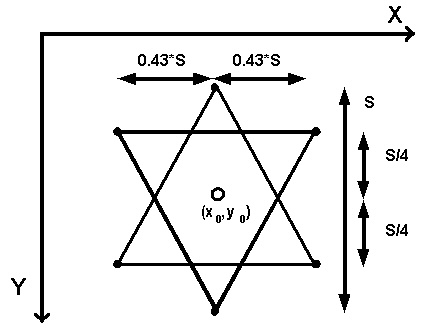
Teken de ster mbv. 2 driehoeken, maar een procedure om een driehoek
te tekenen bestaat er niet. Gebruik hiervoor de Polygon procedure,
die
als
volgt
gedefinieerd is:
PROCEDURE Polygon(n :CARDINAL; px, py :ARRAY OF
INTEGER;
FillColor :CARDINAL; Fill :BOOLEAN);
tekent een polygoon door de n punten te verbinden, waarbij
de x,y coordinaten gegeven zijn in respectievelijk 2 arrays px, py.
Geef
ook
de
kleur mee en of de polygoon opgevuld moet worden.
Om een driehoek te tekenen, creeer 2 arrays van 4 punten en vul deze
met
de hoekpunten van de driehoek. Geef het eerste punt ook mee als laatste
om de driehoek te vervolledigen.
De verhoudingen vind je terug in de tekening (waarbij sin(30 graden)/2
= 1/4 en cos(30 graden)/2 = 0.43)
Tip: om een cardinal met de reele constante 0.43 te
vermenigvuldigen,
moet je deze naar een REAL omzetten. Dit kan je omzeilen door de
cardinal
te vermenigvuldigen als volgt: *43/100.
- Test de procedures uit door een vierkant en een ster in het
midden van
het scherm te tekenen.
S4: Account evolution.
Complete this code.
Implement a procedure AccountEvolution that fills an
array
with
the yearly evolution of a deposit account (zichtrekening). Each
year the invested amount (het belegd bedrag) is raised with the
interest. Use an open array of cardinals as parameter, the initial
amount
and the interest rate. Fill the whole array.
Use the given procedure PrintCardinalArray that prints
a
cardinal
array of arbitrary (willekeurige) size.






S5: Bitmaps
Start with the code from  .
.
We defined:
- the type BitmapAr as two-dimensional arrays of
characters,
where
each element represents a screen pixel.
- three bitmaps gHunter, gEuro &
gBackground
- a colormap (one-dimensional array) where each character is
mapped on a
color.
- a procedure CreateBitmaps() that fills all the
defined arrays.
- Create the procedure DrawBitmap, that draws the bitmap
on a
certain
postion on the screen, pixel by pixel with SetPixel(x,y,color).
Use
a
transparant
background
(the 'z').
- Change the procedure DrawBitmap, so that it draws the
bitmap
on
a certain position on the screen, with a certain background color and
of
a certain pixel size (use Rectangle instead of SetPixel).
These
are
extra
parameters.
- Create a new procedure SumBitmaps that creates a new
bitmap
that
is the drawing of one bitmap on top of the other. Sum gEuro
on
top of gBackground and draw the result.






S6: Permutaties
- Je krijgt 8 punten gedefinieerd in 2 arrays, 1 array voor de
x-waarden
en 1 voor de y-waarden:
x[1] := 201; y[1] := 60;
x[2] := 401; y[2] := 60;
x[3] := 542; y[3] := 201;
x[4] := 542; y[4] := 401;
x[5] := 401; y[5] := 542;
x[6] := 201; y[6] := 542;
x[7] := 60; y[7] := 401;
x[8] := 60; y[8] := 201;
- Gebruik een grafisch scherm van 600 op 600 groot.
- Teken 8 vierkantje van grootte 8 op de gegeven punten.
- Teken een sterretje op de middelpunten van elk koppel punten. Je
moet
dus
alle permutaties uitvoeren tussen de 8 punten.
- Gebruik de procedures gemaakt in S3.






X1: Flikkering.
- Maak 4 arrays van 100 waarden voor:
- x
- y
- grootte
- kleur
- Vul deze arrays met random waarden, gebruik hiervoor de gegeven
RandomCard procedure. Hiervoor heb je de grenswaarden nodig:
- x & y moeten binnen het scherm liggen
- grootte tussen 6 & 16
- Teken nu 1 voor 1 cirkels met de gegeven waarden, zet een delay
van 0.2
s tussen het tekenen van elke cirkel
- Na 8 (= constante SHIFT) cirkels getekend te hebben, maak je de
eerste
weer zwart. Er staan dus steeds SHIFT cirkels op het scherm.
Een beetje moeilijker: als je een cirkel laat verdwijnen, toon je eerst
een ster (zie S3) op die plaats. Dan is het net alsof de cirkel
uiteenspat!






H1: Array Print
- make a procedure that prints an array of integers
- the array can be of any size






H2: String compare
- Make a procedure that compares 2 strings alphabetically and
returns:
- 0 if they are equal
"bla" =
"bla"
- -1 if str1 <
str2
"aap"
<
"als"
- +1 if str1 >
str2
"hops"
>
"hop"
- Remember that a string is terminated with a 0 (use CHR(0), a
procedure
to
convert
a
number into a char). Don't compare the strings after the 0!
- eg: str := ARRAY[1..10] OF CHAR;
- str := "bla";
- The 4th char in str will be a 0, to terminate the word. (str[4]
=
CHR(0))
- Create a type String.
- Use the procedure to compare 2 strings given by the user










PROCEDURE, open arrays, HIGH().
