


TOPIC E: Boolean, real, conversion
Contents :
BOOLEAN, TRUE, FALSE, REAL, /, SQRT, VAL, RdBool,
WrBool, RdReal, WrReal, WrFixReal.
Exercises :
D1: Sinusoide
open Modula2 compiler XDS: start -> programs -> [TW]
Programming ->  XDS environment
XDS environment
copy the  to a new file, run it and try to understand it...
to a new file, run it and try to understand it...
- Teken een sinusoide op het scherm







S1: Equation.
- Los een tweede graadvergelijking op (discriminant
berekenen etc...).
- Gebruik de procedures van de RealMath library, zie

- Let op: alle constantes die je gebruikt in bewerkingen met
REALs, moet je als een REAL definieren:
- schrijf 4.0 ipv 4 in de
discriminantberekening!
- Bereken de oplossingen van volgende vergelijkingen (ax^2 + bx +
c
= 0):
a
b
c #opl?
x1 x2
16.3
2.E-2
-3
8.27
0.24
9.41
3
6 3







S2: Extrapolate (extrapoleren)
The next array is incomplete (start with the  and copy this into your code, AFTER the BEGIN)
and copy this into your code, AFTER the BEGIN)
Arr[0] := -12.34;
Arr[2] := -1.0E1;
Arr[4] := -5.43;
Arr[6] := 5.0E-5;
Arr[8] := 2.903;
Arr[10] := 1.34E1;
Arr[12] := 2.5E1;
Arr[14] := 1.5E1;
Arr[16] := 9.8;
Arr[18] := 3.2;
Arr[20] := -1.0;
- The values for the odd (oneven) index's are missing!
Calculate
them by interpolation:
- take the average of the 2 adjacent (aangrenzende) values.
- print the array.
- Reverse the array without using another array.






S3: Interest.
- Write a program to compute the compound interest on a deposit.
The
principal amount P, interest rate i and the number of years n should
all
be read in from the keyboard.
- The formula for compound interest is:
A = P.(1 + i)^n
- A gives you the amount after n years.
- Show the growth of the amount P for n years. Print the amount
for
each year:
P = 100 euro, the intrest = 5%.
Year 1: 105 euro
Year 2: 110,5 euro
...
- Calculate after how many years your initial amount P has doubled!






S4: Cirkel tekenen
Bestudeer eerst D1
1. Vraag de gebruiker middelpunt en straal van een cirkel en teken
deze, gebruik makend van de parametrische
vergelijking van de cirkel.
x:=
x0 + cos(t) * r
y:=
y0 + sin(t) * r
t:=
1 TO 360
2. Laat het punt 'ronddraaien', meerdere rondjes
3. Verklein de straal stap voor stap, laat het punt draaien tot de
straal
0 is geworden.






X1: Primes.
- Priemgetallen identificeren is een klassieke oefening, er zijn
echter
verschillende manieren om deze te vinden. Voor deze oefening declareer
je
een array van BOOLEAN's. Deze zal diene om het resultaat van de
berekeningen op te slagen. Gezien de array eigenlijk het resultaat
bevat
van je programma is het vanzelfsprekend dat er operaties zullen worden
uitgevoerd
op deze array.
- De interpretatie die je moet toepassen is als volgt: als
er op
de positie met index 4 FALSE staat dan betekent dit dat het getal 4
geen
priemgetal is. Op de positie met index 2 moet dus TRUE staan als alles
goed
verloopt.
a) Zoek zelf hoe je dit zou doen. Denk aan de definitie van een
priemgetal: "een getal dat enkel deelbaar is door 1 en zichzelf". Dit
wil zeggen dat het
getal n een priemgetal is als ik nooit een rest gelijk aan 0 hebt als
ik
n
deel door een getal tussen 2 en n-1.
b) Maak na een programma die de zeef van Erastosthenes
implementeert (zie cursus). Het voordeel van deze oplossing is dat het
veel minder stappen vereist om tot hetzelfde resultaat te komen.
De Zeef van Erastosthenes:
- vul heel de array met TRUE's
- ga dan alle getallen af van de array, start bij 2:
- als het getal nog op TRUE staat:
- is het een priemgetal!
- dan zet je alle veelvouden van dat getal in de array op
FALSE (zo
elimineer je alle niet-priemgetallen)
- je bekomt zo een dubbele lus.






H1: Canon
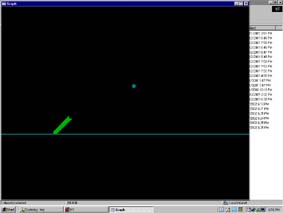
- Maak een kanon die kogels afvuurt.
- Vraag de gebruiker de hoek van het kanon (in graden tussen 0 en
90)
en de beginsnelheid van de kogel (tussen 0 en 50m/s).
- Teken het kanon (mbv een lijn is OK) en laat de kogel vertrekken
wanneer je op ENTER duwt.
- Gebruik de volgende constantes:
CONST
PI = 3.14;
TIJDSTAP = 0.025; (* in seconds*)
STRAAL_KOGEL = 7; (* in pixels *)
g =
9.81; (* m/s2*)
SCALE =
5.0; (* in pixels/m, dus het scherm
stelt ongeveer 100m voor *)
- Ook
nog volgende gekende formules:
radialen = 2Pi * graden/360
x = x0 + vx.t
y = y0 - vy . t + g.t .t /2






H2: Ganzenbord
In het alom bekende ganzenspel heeft elke speler een pion en moet vanaf
de
start de finish (in ons geval: op vakje 63 of erover komen) bereiken
over
een ganzenbord.
Het ganzenbord bestaat uit positieve en negatieve hindernissen. Een
speler
gooit met 2 dobbelstenen om te bepalen hoeveel vakjes hij in die beurt
vooruit
mag gaan. Als hij dan op een positieve hindernis terecht komt,
mag
hij een aantal vakjes extra vooruit gaan. Bij een negatieve hindernis
moet
hij een aantal vakjes achteruit. Dit moet hij te doen tot hij op een
neutraal
vakje komt, dan is zijn beurt pas afgelopen.
Copieer deze code.
P staat initieel op vakje 0 en moet voorbij het vakje 62 komen. We
hebben
al met de dobbelstenen d1 & d2 gesmeten en de resultaten hiervan in
2
arrays (d1 & d2) gestoken. Dus voor de eerste beurt van P moet je
het
eerste element van d1 & d2 nemen als resultaat van zijn worp, enz.
Er
zijn 12 worpen gegeven, maar het is niet zeker dat ze allemaal nodig
zijn!
Je mag er van uit gaan dat het er niet meer dan 12 zullen zijn.
De vraag luidt:
- laat zien hoe P het ganzenbord afloopt
- in hoeveel beurten geraakt hij voorbij de
finish?
- wat is het gemiddeld aantal vakjes die hij
per
beurt heeft gesprongen?







T1
- Ga na op papier hoeveel maal de lijn "x := 1;"
wordt
uitgevoerd bij het runnen van dit programma? Ik wil een getal + een
bondige
verklaring voor dit resultaat.
- Check daarna uw oplossing door het programma te runnen! Pas het
aan zodat het resultaat geprint wordt.
- Check uw programma ook met de debugger!
MODULE T1;
<* NOOPTIMIZE + *>
FROM IO IMPORT WrStr, WrLn, WrInt, WrChar, WrCard, WrReal;
CONST MAX = 6;
VAR
i, j, x: CARDINAL;
BEGIN
WrLn;
i := MAX;
REPEAT
FOR j := (i * 2) TO 1 BY -2 DO
x := 1; (*** hoeveel malen wordt dit
uitgevoerd??
***)
END;
i := i - 2;
UNTIL (i = 0);
END T1.










