topic G

TOPIC G: Records

Exercises :

(D1) Sum of Complex numbers

(S1) Complex Product

(S2) Adjacent pieces (aangrenzende stukken).

(S3) Toren.

(S4) FiguurTekenaar.

(S5) Lopend Manneke

(S6) Botsende biljartballen.

(X1) Zonnestelsel

(H1) Words in a sentence.

(H2)

(T1) Output

(T2) Output

Some useful hints!

D1: Sum of Complex numbers.

copy the

to a new file, run it and try to understand it...

define two complex numbers:

c1 = 3,5 - 4,76i
c2 = 4 - 4,6i

calculate the sum of c1 & c2 with a third variable and print out the result.

S1: Complex Product.

Start with

Define a new type ComplexRc, use it to redefine c1, c2 and c3.
Make a procedure that prints a complex number (use the type ComplexRc) and replace the code that prints c1, c2 & c3.
Make a procedure that multiplies 2 complex numbers. Use it to multiply c1 and c2.

S2: Adjacent pieces (aangrenzende stukken)

An (imaginery) game is played by 2 players, black & white, who both have 8 pieces on a 6 by 6 board. This is the board with the pieces (B for black and W for white).

CONST MAX = 6;

board: ARRAY[1..MAX],[1..MAX] OF CHAR;

board[1] := "--B-B-";
board[2] := "W-BW--";
board[3] := "W-W--B";
board[4] := "--B--W";
board[5] := "WW---B";
board[6] := "B--B-W";

For the game it is important to know all the pieces:

Create a datastructure which can hold all the pieces plus the relevant properties of each piece: its number, its colour ('B' or 'W'), its position.
Check the whole board, fill the datastructure and print it out.
The resulting datastructure is an array of records, with a record for each piece on the board. The output will be a table:

Piece Colour x y

----- ------ --- ---

1 B 1 3

2 B 1 5

3 W 2 1

4 B 2 3

...

16 W 6 6

Add the number of adjacent pieces to the properties of each piece.

Adjacent is defined as above, under, to the left or to the right (4 positions, niet schuin dus)
Tip: to check the adjacent pieces, watch out not to fall out of the board (invalid index-crash)! Find a solution for this!
The output will become:

Piece Colour x y nbrAdjacent

----- ------ --- --- -----------

1 B 1 3 1

2 B 1 5 0

3 W 2 1 1

4 B 2 3 3

...

16 W 6 6 1

S3: Toren.

We wensen een toren van 2.5m te bouwen door het opstapelen van kubussen.

De onderste kubus heeft een ribbe van 1m, de volgende kubussen zijn telkens 2/3 kleiner.

opgelet: als je 1m als CARDINAL schrijft, in centimeters bvb, dan geeft 2/3*... problemen, immers wordt 2/3 = 0.666 afgerond tot 0 (is immers een cardinal)

Stapel de kubussen opeen tot je toren net hoger is dan 2.5m.

Stokeer alle kubussen in een datastruktuur, waarbij je van elke kubus de lengte van de ribbe bijhoudt en de hoogte tot de grond (de eerste staat op de grond, de hoogte is dus 0m, de tweede staat op 1m).

Hoeveel kubussen heb je nodig?

Teken de kubussen mbv de Vierkant procedure (zet x = een constante). Neem 2.5m = schermgrootte = 500pixels => 1m = 200 pixels.

S4: FiguurTekenaar.

Gegeven zijn procedures om de volgende figuren te tekenen: cirkel, ellips, vierkant, ster en driehoek.
Maak een programma die figuren tekent door aan de gebruiker te vragen welke figuur hij wilt, met welke kleur en deze figuur dan op een willekeurige positie tekent met een willekeurige grootte.
Een procedure om een willekeurig getal te genereren is ook gegeven.

Copieer deze code en bestudeer de gegeven procedures.
Definieer een figuur-type met de volgende eigenschappen: figuurtype, middelpunt, grootte en kleur.
Vraag de gebruiker welke figuur hij wilt en met welke kleur, vul de waarde in een figuur-variabele.
Maak een TekenFiguur procedure die deze figuur tekent: een procedure die een figuur (zoals in punt 2 gedefinieerd) als input neemt.
Genereer dan random waarden voor middelpunt en grootte, en teken de figuur.
Zet bovenstaande in een lus: teken figuren tot de gebruiker 0 intikt voor de kleur.

S5: Lopend Manneke.

Start met de code van

.
Gegeven is het record LedemaatRc die een been van het manneke voorstelt, ook de procedure om deze te tekenen is gegeven.
Gevraagd:

Teken een manneke met 2 benen gedefinieerd door 2 ledemaat records
Zet deze code dan in een procedure en definieer een record dat zo'n manneke voorstelt (eigenschappen: positie, grootte, hoek van benen, kleur)
Teken dan het manneke en laat het zich vooruit lopen door de benen 'correct' te bewegen.
Zorg dat het manneke links weer verschijnt als het rechts van het scherm verdwijnt
Zorg dat de gebruiker de snelheid van het manneke kan regelen:

sneller als hij '+' indrukt, trager voor een '-'
Gebruik:
PROCEDURE KeyPressed():BOOLEAN;
Procedure geeft TRUE als er een toets werd ingedrukt. Deze procedure blijft TRUE geven, zolang de ingedrukte toets niet uit de ‘inputbuffer’ gelezen wordt met de volgende procedure:
PROCEDURE RdKey(): CHAR;
Met deze procedure lees je een ingedrukte toets uit de inputbuffer. Als de inputbuffer leeg is, wacht deze procedure tot er op een toets gedrukt wordt.

Uitbreidingen: teken er bewegende armpjes bij, ...

S6: Botsende BiljartBallen

Deze oefening gaat verder op 'Bewegende Circels', Topic D S6.
1. Gebruik de gegeven array van records als coordinaten x,y voor het middelpunt en grootte g om er circels mee te tekenen. Gebruik vx, vy voor de snelheidsvector, die bepaalt in welke richting de circels bewegen. Hint: gebruik integers voor de coordinaten, dit zal het vervolg van de oefening vergemakkelijken.

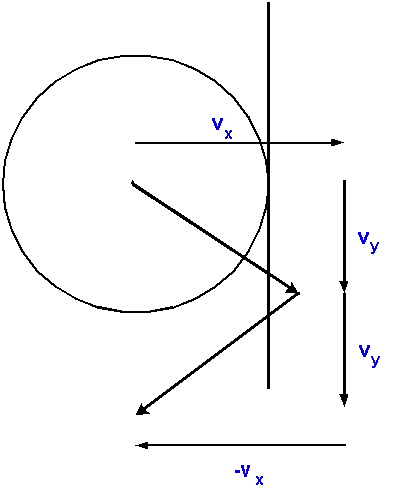
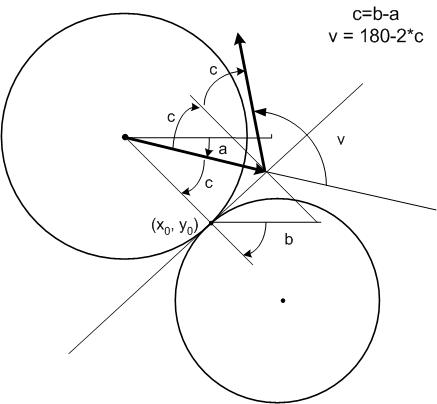
CONST SIZE=10;

a[1].x := 200; a[1].y := 300; a[1].g := 10; a[1].vx := 5; a[1].vy := 4;
a[2].x := 123; a[2].y := 456;a[2].g := 20; a[2].vx := 2; a[2].vy := -2;
a[3].x := 512; a[3].y := 500; a[3].g := 30; a[3].vx := -3; a[3].vy := -1;
a[4].x := 123; a[4].y := 50; a[4].g := 25; a[4].vx := 3; a[4].vy := 0;
a[5].x := 432; a[5].y := 300; a[5].g := 15; a[5].vx := -3; a[5].vy := 1;
a[6].x := 234; a[6].y := 670; a[6].g := 12;a[6].vx := 2; a[6].vy := -3 ;

2. Gebruik de gegeven Arrow procedure om de snelheidsvectoren te tekenen. Deze procedure staan in onze StandardLib, deze vind je op de Modula-2 technology pagina. Download de .def en .mod file naar de folder met je eigen module. Dan kan je simpelweg procedures importeren van StandardLib:

FROM StandardLib IMPORT Arrow;

Uitleg over de werking van libraries (en hoe er zelf te maken) vind je onder de Modula-2 documentatie: XDS manual

3. Laat de circels botsen als ze de rand van het scherm raken. Je moet dan enkel de richting van 1 snelheidscomponent omdraaien:

4. Laat de circels botsen als ze elkaar raken, net als biljartballen. Gebruik de procedures Distance (afstand), AngleWithXAx (om de hoeken te berekenen) en RotatePoint (om de snelheidsvector te draaien):

X1: Zonnestelsel

Simuleer de dynamiek van een Newtoniaans stelsel van massa's, in 2 dimensies!
Het is wenselijk eerst de kanon-oefening op te lossen.

Maak een datastructuur voor een planeet, geef het de volgende eigenschappen:

massa (in kg)
grootte (in m), deze is gerelateerd met de massa
positie (2 dimensies)
snelheid (m/s)
totale kracht (Newton)
volgende positie (dit zal handig zijn voor het tekenen)

Maak een array van planeten. Initialiseer de waarden.
Teken de planeten, laat de tijd in discrete stappen (TIJDSTAP) vorderen mbv volgende formules:

F = som Fi (vektor!!)

|F| = G.m.Mi/r^2

G = 6.67E-11N.m^2/kg^2

alfa = arctan((y2-y1)/(x2-x1)) (gebruik de AngleWithXAx procedure van S6)
Fx = |F|.cos(alfa)
Fy = |F|.sin(alfa)
r = afstand

a = F/m
volgende positie = positie + v.TIJDSTAP + a.TIJDSTAP^2/2
nieuwe snelheid = snelheid + a.TIJDSTAP

Teken ook de vectoren van snelheid en totale kracht (procedure om een pijltje te tekenen).

Dan bekom je zo iets (oplossing John Lataire & Stijn Vastiau): uiteenvliegen & planetenballet

H1: Words in a sentence.

Define a string sent which can contain a sentence of 100 letters.

Fill the variable:

sent := "The end of the world was programmed in MODULA2 for 31-12-99!?";

Define a datastructure that can contain 5 records. The records have the following fields:

word: can contain a word upto 10 characters
length: contains the length of the word
present (aanwezig): a boolean
start: a cardinal

Fill the array:

arr[1].word := "the";

arr[1].length := 2;

arr[2].word := "war";

arr[2].length := 3;

arr[3].word := "word";

arr[3].length := 4;

arr[4].word := "for";

arr[4].length := 2;

arr[5].word := "rammed";

arr[5].length := 6;

Write an algorithm that fills the field present of the 5 elements of the array with a TRUE if the word appears in the sentence (case sensitive match), with FALSE otherwise. Furthermore, if the word appears, fill the field start with the place where the word starts in the sentence (starting from 1). If the word doesn't appear in the sentence, fill start with a 0. (stop the search if you have found an occurence, you don't need to look for a second one)
Print the array results for the fields present and start like this:

Word 1 appears in the sentence at place 12.
Word 2 does not appear in the sentence.
..."

H2:

T1: Output

What is the output of the following program?

MODULE T1;<* NOOPTIMIZE + *>
FROM IO IMPORT RdChar, WrChar, WrStr, RdStr, WrLn, RdCard, WrCard, RdInt, WrInt, RdReal, WrReal, RdBool, WrBool;

    CONST
       MIN = 2;
       MAX = 3;          (* constants *)

    TYPE Rc = RECORD
                 a, b: INTEGER;
              END;
         Ar = ARRAY[MIN..MAX] OF INTEGER;

    PROCEDURE Proc1(a, b, c: INTEGER): BOOLEAN;
      VAR toReturn: BOOLEAN;
    BEGIN
      a := a + b + 1;
      IF a > c THEN
        toReturn := TRUE;
      ELSE
        toReturn := FALSE;
      END;
      RETURN toReturn;
    END Proc1;

    PROCEDURE Proc2(a, b, c: INTEGER): INTEGER;
      VAR toReturn: INTEGER;
    BEGIN
      IF c > b THEN
        toReturn := (a + b) ;
      ELSE
        toReturn := (a + c) ;
      END;
      RETURN toReturn;
    END Proc2;

    PROCEDURE WrRc(c: Rc);
    BEGIN
      WrStr("field a = ");WrInt(c.a,0);WrLn;
      WrStr("field b = ");WrInt(c.b,0);WrLn;
    END WrRc;
    PROCEDURE WrAr(c: ARRAY OF INTEGER);
    (* procedure that prints the array *)
      VAR i: CARDINAL;
    BEGIN
      FOR i := 0 TO HIGH(c) DO
        WrStr("El ");WrCard(i,0);WrStr(" = ");WrInt(c[i],0);WrLn;
      END;
    END WrAr;

    VAR c:Rc;            (* variable-declarations *)
        d:Ar;
BEGIN
    WrLn;
    c.a := 1;
    c.b := 2;
    d[2] := 3;
    d[3] := 4;

    WHILE Proc1(c.b, d[2], c.a) DO
      c.a := Proc2(d[2], d[3], c.b);
      DEC( d[2]);   (* definition of Decrement: DEC(n); is similar as n := n - 1; *)
      DEC( d[3]);
    END;
    WrRc(c);
    WrAr(d);
END T1.

T2: Output (more difficult)

What is the meaning of the calculated n's in the following program?
An ID is a unique number to identify a record (een uniek nummer om een record te identificeren), in this program it is also its index in the array.
WATCH OUT: it makes no sense to run this program, the arrays aren't filled, so there will be no meaningfull output.

MODULE T2;
<* NOOPTIMIZE + *>
FROM IO IMPORT WrLn, WrCard, RdCard;
CONST
    MAX_NAME_SIZE = 30;
    NBR_TEACHERS = 5;
    NBR_COURSES = 20;
    NBR_GROUPS = 15;
    TIME_THEORY_EXAM_PER_STUDENT = 0.5; (* in hours *)

VAR
    teachers: ARRAY[1..NBR_TEACHERS] OF RECORD
                                           id: CARDINAL;
                                           name: ARRAY[1..MAX_NAME_SIZE] OF CHAR;
                                         END;
    courses: ARRAY[1..NBR_COURSES] OF RECORD
                                          id: CARDINAL;
                                          name: ARRAY[1..MAX_NAME_SIZE] OF CHAR;
                                          teacherID: CARDINAL;
                                          duration: CARDINAL; (* in hours *)
                                          isTheory: BOOLEAN; (* if FALSE: it is a practicum course *)
                                         END;
    studentGroups: ARRAY[1..NBR_GROUPS] OF RECORD
                                           id: CARDINAL;
                                           nbrStudents: CARDINAL;
                                           nbrCourses: CARDINAL; (* nbr of courses of the group *)
                                           courseIDs: ARRAY[1..NBR_COURSES] OF CARDINAL; (* courses of the group *)
                                          END;
    te, co, gr, coID: CARDINAL;
    n1, n2, n4, n5: CARDINAL;
    n3 : REAL;

BEGIN
(*
arrays of records are filled here ...
*)
n1 := 0; n2 := 0; n3 := 0.0; n4 := 0, n5 := 0;

FOR te = 1 TO NBR_TEACHERS DO
FOR co = 1 TO NBR_COURSES DO
IF courses[co].teacherID = te THEN

        IF courses[co].isTheory THEN
          INC(n1);
          n2 := n2 + courses[co].duration;
          FOR gr := 1 TO NBR_GROUPS DO
            FOR coID = 1 TO studentGroups[gr].nbrCourses DO
              IF studentGroups[gr].courseIDS[coID] = co THEN
                n3 := n3 + VAL(REAL, studentGroups[gr].nbrStudents) * TIME_THEORY_EXAM_PER_STUDENT;
              END;
            END;
          END;

        ELSE (* practicum *)
          FOR gr := 1 TO NBR_GROUPS DO
            FOR coID = 1 TO studentGroups[gr].nbrCourses DO
              IF studentGroups[gr].courseIDS[coID] = co THEN
                INC(n4);
                n5 := n5 + courses[co].duration;
              END;
            END;
          END;
        END;

      END;
    END;
    WrStr("Load of teacher ");WrStr(teachers[te].name);WrStr(" is:");WrLn;
    WrStr("... is ");WrCard(n1,0);WrLn;
    WrStr("... is ");WrCard(n2,0);WrStr(" hours");WrLn;
    WrStr("... is ");WrReal(n3,4, 0);WrStr(" hours");WrLn;
    WrStr("... is ");WrCard(n4,0);WrLn;
    WrStr("... is ");WrCard(n5,0);WrStr(" hours");WrLn;
END;
END T2.