Practical Parallel Programming - Project

main page - practicum

• Objectives
• Organization
• Topics

Objectives

For a (frequently occurring) computational problem you should develop different parallel solutions, at least the ones discussed in the practica: vectorization, multi-threading and message-passing.

• Implement or get the sequential version.
  
• Create naive, parallel implementations with the 3 techniques. Do not optimize, just make sure everything works and the result is correct.
  
• Compare the result of all your parallel implementations with the sequential one. Also measure speedup, performance (flops) and bandwidth. We advice you to make some management code (or script) that automates this!
•  Start with the MPI-MT code that can be found on the Hydra doc page.
  
• Optimize the naive implementation by trying to overcome the anti-parallel patterns (inefficiencies) it contains.
• Study alternative implementations and compare their performance.

Organization

Here are the rules for the project:

• The project will be under the guidance of mainly Jan Lemeire (and Nick Wouters).
• You can work alone or in groups of two.
• The deadline to choose a topic is December 13th, 2024.
• Meet us (make an individual appointment which can be via Teams):
• once you have the sequential code + ideas about the parallelization. To discuss the ideas and put you on the right track.
  
• somewhere halfway the project to discuss your current problems, to let us give advice and to define the expected end result.
  
• The deadline for the project is 3 days before the oral exam in January.

We expect the following deliverables:

• All relevant code related to the project.
• sequential code + parallel implementations
  
• the parallel versions should check their result with the one of the sequential version to proof that the outcome is correct!
• Remove object and exe-files (and all other intermediate files). Use Build -> clean for instance and remove the .vs folder manually. Minimally, we need source files, and solution (.sln) and project file (.vcxproj).
• A short report that describes:
  • The problem (brief).
  • The different implementations. You can be brief here, since we have your source code. A diagram or scheme might be helpful here.
    
  • Links to sources of information and of source code.
  • Description of the parallel system used:
    
  • CPUs: use CPU-Z for instance to get hardware details
    
  • HYDRA: which CPUs were used
    
  • Most important: a discussion of the performance of the different implementations
  • Give speedups, computational performance (flops) and bandwidth of the different experiments
  • MPI: determine the granularity (computation versus communication) of your program.
    
  • Graphs:
    
  • MPI and multithreaded: speedup in function of p (number of processes/threads)
    
  • all: speedup in function of W (problem size, which is a problem-dependent parameter)
  • which implementations are scalable?
    
  • Discussion of results: compare implementations and try to explain inefficiencies
  • especially in case of bad speedups, try to find out why it is performing so bad
    

Topics

1. Reductions: sum, product, mul-add or max of an array.
   
1. Compare with a non-reduction operation having the same number of computations. E.g. compare the global sum with adding a constant to all elements of a vector. The number of operations is the same, except that the reduction needs a specific structure with synchronization.
   
2. Sorting. Although an very common algorithm, it will still be interesting to see some results. For vectorization, some special intrinsic functions exist.
3. Convolutions, like a sobel filter or a Gaussian blur. With large filters good speedups can be achieved.
• Variant: simulation of temperature evolution. Sequential code.
  
4. Discrete Optimization Problem. Choose a problem, like the shift puzzle explained here. See the theory chapter devoted to it.
   
5. Genetic algorithms.
   

More topics

Topics 2016-2017 (click here)

a) Pattern recognition in signals

Consider the following large, historical 1D signal consisting of 2 variables that fluctuate in time:

Let's index the two arrays as follows:

Now we want to find matches of a given, limited signal - the query - in the historical data.
Example:

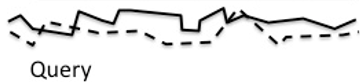
Indexed as follows:



To find a match we slide the query over the historical data and for each offset calculate the distance between both:
  => 
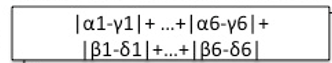Here the sum of absolute differences is taken as distance metric.

• Many algorithms consist of basic operations on matrices and vectors.
• Consider the following code (which is part of a single value decomposition) in which a, u and v are large matrices:

for (i=n;i>=1;i--) {
    if (i < n) {
        if (g) {
            for (j=l;j<=n;j++) Double division to avoid possible underflow.
                v[j][i]=(a[i][j]/a[i][l])/g; // (*) calculating column
            for (j=l;j<=n;j++) {
                for (s=0.0,k=l;k<=n;k++) s += a[i][k]*v[k][j]; // (*) row x column (reduction)
                for (k=l;k<=n;k++) v[k][j] += s*v[k][i];  //(*) factor x column
            }
        }
        for (j=l;j<=n;j++) v[i][j]=v[j][i]=0.0;  // (*) setting column and row
    }
    v[i][i]=1.0;
    g=rv1[i];
    l=i;
}

• We observe that the basic operations (*) are operations on rows and columns.
• Porting this code to the GPU starts by moving the matrices to the GPU and for each basic operation do a kernel call. We simply need a OpenCL library for basic matrix and vector operations. This will already give a decent speedup for big matrices.
• Note that the reduction (second *) is a not so easy to optimize problem. Luckily this has been done already. You can reuse this code, although you might have to change it to make it a global sum over products.
  
• Next, the code can be optimized by:
• kernel fusion: in the third for-loop 2 kernels are called. They could be merged into 1 kernel (or not?).
• parallelizing for-loops: the second and third for-loop can run independently, hence they can be parallelized.
• ...
• Measure the performance gain of each optimization.
  
• We can give other examples of such algorithms. There are enough issues to be solved and tested such that multiple students can work on this.
  
• Ultimate goal: design a general methodology to handle such algorithms in general.
  

c) Solving linear equations

• Many problems boil down to solving a set of linear equations. This can be written as A.x = B, with x a n-dimensional vector which is unknown, B a m-dimensional vector and A a nxm matrix. A and B are given, find x.
• Several solutions exist to solve this (we have a reference book with c-code for all solutions):
• Jacobi
• Gauss-seidel
  
• Gaussian elimination with backsubstitution
• LU decomposition
  
• Single value decomposition (the previous topic)
• ...
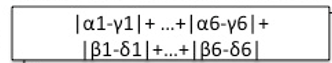