Parallel Systems Project

main page

• Objectives
• Organization
• Topics

Objectives

For a (frequently occurring) computational problem you should develop 3 parallel solutions, namely with each of the 3 basic techniques: multi-threading, message-passing and OpenCL.

• Implement or get the sequential version.
  
• Create naive, parallel implementations with the 3 techniques. Do not optimize, just make sure everything works and the result is correct.
  
• Compare the result of all your parallel implementations with the sequential one. Also measure speedup, performance (flops) and bandwidth. We advice you to make some management code (or script) that automates this!
  
• Optimize the naive implementation by trying to overcome the anti-parallel patterns (inefficiencies) it contains.
• Study alternative implementations and compare their performance.

Organization

Here are the rules for the project:

• The project will be under the guidance of Jan G. Cornelis and Jan Lemeire.
• You can work alone or in groups of two.
• The deadline to choose a topic is November 17, 2017.
• Meet us somewhere halfway the project to discuss your current problems, to let us give advice and to define the expected end result. Make an individual appointment.
  
• The deadline for the project is December 15, 2017.

We expect the following deliverables:

• All relevant code related to the project.
• sequential code + parallel implementations
  
• the parallel versions should check their result with the one of the sequential version to proof that the outcome is correct!
  
• A short report that describes:
  • The problem (brief).
  • The different implementations. You can be brief here, since we have your source code. A diagram or scheme might be helpful here.
    
  • Links to sources of information and of source code.
  • Description of the parallel system:
    
  • CPUs: use CPU-Z for instance to get hardware details
    
  • GPUs: Benchmark the GPU with our microbenchmarks, submit the results to our database.
    
  • Most important: a discussion of the performance of the different implementations
  • Give speedups, computational performance (flops) and bandwidth of the different experiments
  • MPI: determine the granularity (computation versus communication) of your program.
    
  • GPU: Determine the computational intensity of your kernel to know whether it is memory bound or computation bound or both. The roofline model will be briefly discussed during the last exercise session using this visual studio solution .
  • Graphs:
    
  • MPI and multithreaded: speedup in function of p (number of processes/threads)
    
  • all: speedup in function of W (problem size, which is a problem-dependent parameter)
  • which implementations are scalable?
    
  • Discussion of results: compare implementations and try to explain inefficiencies
  • especially in case of bad speedups, try to find out why it is performing so bad
    
• A small presentation for the other students and ourselves.The presentation will be given by the end of December.
  

Topics

1. Sorting. Although an very common algorithm, it will still be interesting to see some results. For instance, test bitonic sort on the GPU! See the theory chapter devoted to it.
2. Discrete Optimization Problem. Choose a problem, like the shift puzzle of the theory (we have sequential java code you can start from!). See the theory chapter devoted to it. Using the power of a GPU is a challenge here, there are several options.
   
3. Genetic algorithms.
   

Previous topics (which you can still choose)

Topics 2016-2017 (click here)

For each topic we will give some pointers to problem descriptions together with a number of possible implementations.
We will also try to give an estimation of the difficulty level and feasibility.

Topics 2014-2015

For each topic we will give some pointers to problem descriptions together with a number of possible implementations.
We will also try to give an estimation of the difficulty level and feasibility.

a) Pattern recognition in signals

Consider the following large, historical 1D signal consisting of 2 variables that fluctuate in time:

Let's index the two arrays as follows:

Now we want to find matches of a given, limited signal - the query - in the historical data.
Example:

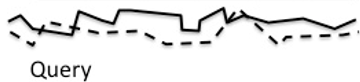
Indexed as follows:



To find a match we slide the query over the historical data and for each offset calculate the distance between both:
  => 
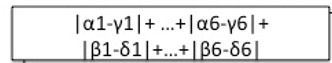Here the sum of absolute differences is taken as distance metric.

b) OpenCL-OpenGL integration for processing and viewing 3D images

• Apply image algorithms (to be discussed) on 3D images (OpenCL) and be able to browse through them (OpenGL)
• You can let OpenCL and OpenGL work on the same data. It would also be nice to interactively (via OpenGL) initiate operations implemented in OpenCL.
  
• We have code you can start with.

c) Algorithms on matrices

• Many algorithms consist of basic operations on matrices and vectors.
• Consider the following code (which is part of a single value decomposition) in which a, u and v are large matrices:

for (i=n;i>=1;i--) {
    if (i < n) {
        if (g) {
            for (j=l;j<=n;j++) Double division to avoid possible underflow.
                v[j][i]=(a[i][j]/a[i][l])/g; // (*) calculating column
            for (j=l;j<=n;j++) {
                for (s=0.0,k=l;k<=n;k++) s += a[i][k]*v[k][j]; // (*) row x column (reduction)
                for (k=l;k<=n;k++) v[k][j] += s*v[k][i];  //(*) factor x column
            }
        }
        for (j=l;j<=n;j++) v[i][j]=v[j][i]=0.0;  // (*) setting column and row
    }
    v[i][i]=1.0;
    g=rv1[i];
    l=i;
}

• We observe that the basic operations (*) are operations on rows and columns.
• Porting this code to the GPU starts by moving the matrices to the GPU and for each basic operation do a kernel call. We simply need a OpenCL library for basic matrix and vector operations. This will already give a decent speedup for big matrices.
• Note that the reduction (second *) is a not so easy to optimize problem. Luckily this has been done already. You can reuse this code, although you might have to change it to make it a global sum over products.
  
• Next, the code can be optimized by:
• kernel fusion: in the third for-loop 2 kernels are called. They could be merged into 1 kernel (or not?).
• parallelizing for-loops: the second and third for-loop can run independently, hence they can be parallelized.
• ...
• Measure the performance gain of each optimization.
  
• We can give other examples of such algorithms. There are enough issues to be solved and tested such that multiple students can work on this.
  
• Ultimate goal: design a general methodology to handle such algorithms in general.
  

d) Solving linear equations

• Many problems boil down to solving a set of linear equations. This can be written as A.x = B, with x a n-dimensional vector which is unknown, B a m-dimensional vector and A a nxm matrix. A and B are given, find x.
• Several solutions exist to solve this (we have a reference book with c-code for all solutions):
• Jacobi
• Gauss-seidel
  
• Gaussian elimination with backsubstitution
• LU decomposition
  
• Single value decomposition (the previous topic)
• ...
  

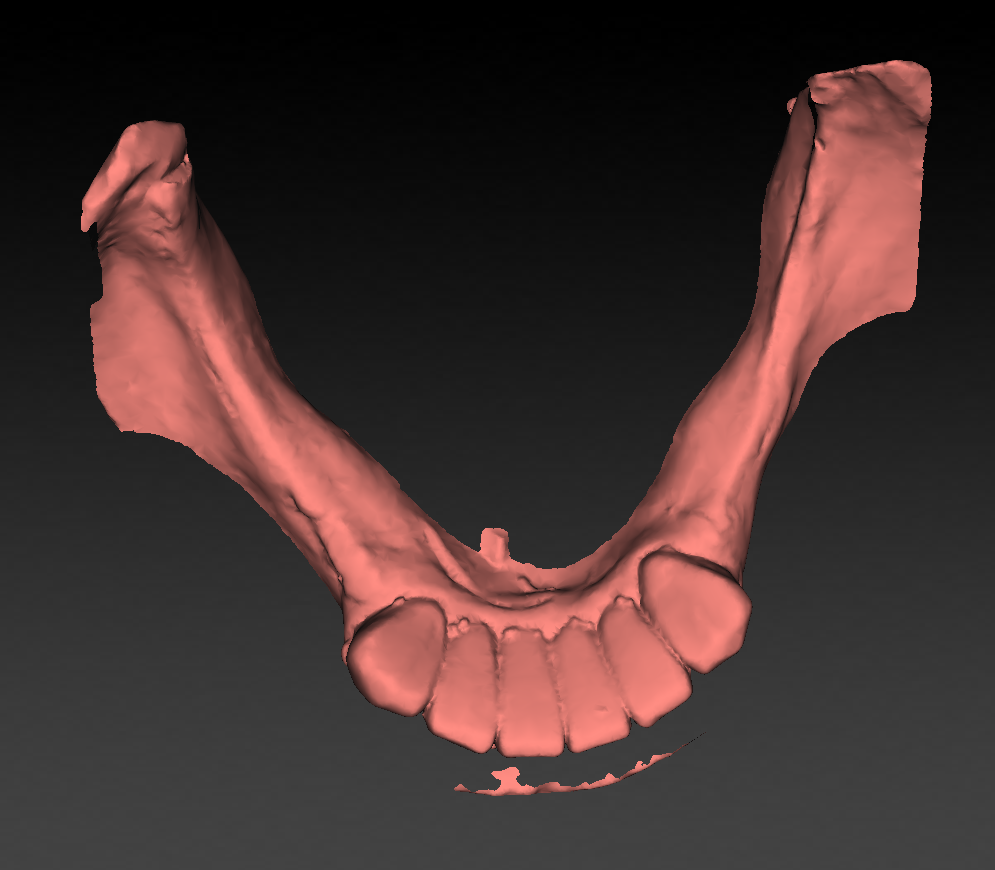
e) Tree Construction and Tree Traversal (can be split into 2 separate topics)

• Given a mesh of vertices (forming triangles) describing a 3D volume:

• We want to know in each point in space the distance to the volume, i.e. the distance to the closest vertex/triangle:

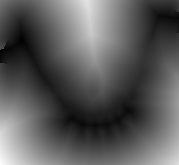
• A naive way to do this is to traverse for each point in space over all vertices and find the closest one.
• If the mesh contains about 1 million vertices and for the space 512x512x512 points are considered, this will take ages...
• Finding the closest vertex fast happens by tree describing a Bounding Volume Hierarchy:
• the tree and tree traversal is explained here (although it is not exactly the same problem).
• construction of the tree is explained here.
• CUDA-code is provided. Use if for our problem, make it OpenCL and think about optimizations. On a CPUquadcore i7 the above mesh takes 15 minutes to complete... On a GPU?
  
• we will provide you the data.
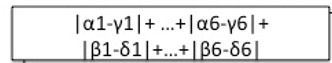