Topic E

TOPIC E: Records

Exercises :

(D1) Som van Complex getallen

(S1) Complex Product

(S2) Lopend Manneke

(S3) Flight Simulator.

(H1) FiguurTekenaar.

(H2) Zwaartepunt

(T1) Output

(T2) Scope

D1: Som van Complexe getallen.

Bekijk het programma van hier:

Het definieert 2 complexe getallen:

c1 = 3,5 - 4,76i
c2 = 4 - 4,6i

en berekent de som van c1 & c2 met een derde variabele.

D2 types: Definieer een nieuw type ComplexRc, gebruik dit om c1, c2 en c3 te declareren.

S1: Complex Product.

Start met D2:

Maak een procedure dat een complex getal print (gebruik het type ComplexRc) en vervang de code die c1, c2 & c3 print.
Maak een procedure die 2 complexe getallen vermenigvuldigt. Bereken het product van c1 en c2.

S2: Lopend Manneke.

Start met de code van

.
Gegeven is het record LedemaatRc die een been van het manneke voorstelt, ook de procedure om deze te tekenen is gegeven.
Gevraagd:

Teken een manneke met 2 benen gedefinieerd door 2 ledemaat records
Zet deze code dan in een procedure en definieer een record dat zo'n manneke voorstelt (eigenschappen: positie, grootte, hoek van benen, kleur)
Teken dan het manneke en laat het zich vooruit lopen door de benen 'correct' te bewegen.
Zorg dat het manneke links weer verschijnt als het rechts van het scherm verdwijnt
Zorg dat je de snelheid van het manneke kan regelen:

sneller als hij '+' indrukt, trager voor een '-'
Gebruik:
PROCEDURE KeyPressed():BOOLEAN;
Procedure geeft TRUE als er een toets werd ingedrukt. Deze procedure blijft TRUE geven, zolang de ingedrukte toets niet uit de ‘inputbuffer’ gelezen wordt met de volgende procedure:
PROCEDURE RdKey(): CHAR;
Met deze procedure lees je een ingedrukte toets uit de inputbuffer. Als de inputbuffer leeg is, wacht deze procedure tot er op een toets gedrukt wordt.

Als het manneke aan het einde van het scherm komt, moet hij terugkeren. Gebruik hiervoor de naarLinks boolean die de richting van de voetjes aangeeft.
Het programma moet stoppen als je op 'x' duwt.

Uitbreidingen: teken er bewegende armpjes bij, ...

S3: Flight Simulator.

Start met deze code. Gegeven zijn 2 record types en 2 procedures.
Dit document legt uit hoe je op een simpele manier een 3D-landschap tekent. De formules van de laatste pagina vertellen hoe je 3D-coordinaten omzet naar een 2D-punt op je scherm.

Schrijf een procedure die de omzetting van een 3D punt naar 2D punt berekent.
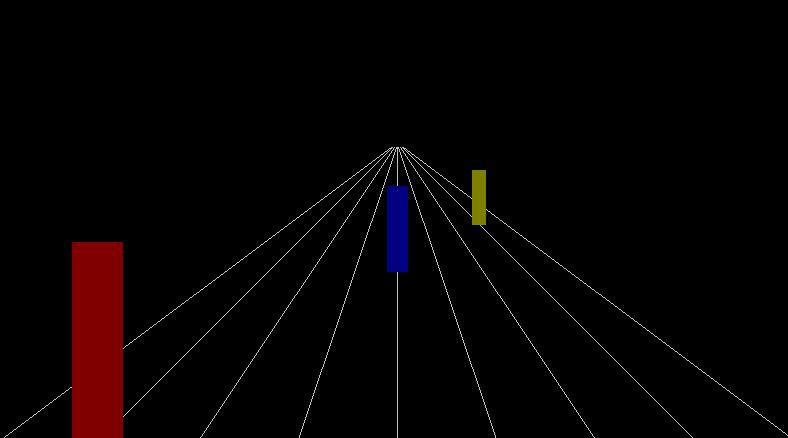
Maak een procedure die om de 100 pixels een lijn tekent tot aan de horizon (zie linkse figuur). Gebruik de gegeven Line2 procedure. Deze zorgt ervoor dat je programma niet crasht als je buiten het scherm tekent.

Tip: Je kan snel een record creëren met Point{x, y, z}

Maak een procedure die een rechtopstaande rechthoek tekent met gegeven het middelpunt van de bovenste zijde, de breedte en de kleur. Gebruik de gegeven Rectangle2 procedure.
Teken met deze procedure enkele rechthoeken (zie rechtse figuur).
Zorg ervoor dat je door het nu gedefinieerd landschap kunt 'vliegen'. Dat je vooruit, naar links, naar rechts en naar boven en beneden kunt bewegen met de toetsen. Dit doe je door de coördinaten van het zichtspunt (dx, dy, dz) af te trekken van het 3D punt (de parameter) in je omreken procedure. Definieer dit punt als een globale variabele (helemaal bovenaan). Zorg ervoor dat het programma stopt als je op 'q' drukt.

Dan bekom je zo iets
Opgelet: door vooruit te stappen worden de lijnen 'achter je' verder getekend, dit zorgt echter snel voor problemen dat de getallen te groot worden (groter dan maximale waarden). De oplossing is de lijnen pas vanaf dy te tekenen.

Vlieg tegen een bepaalde snelheid die de gebruiker kan aanpassen (versnellen of vertragen).
Optioneel: Om er een flight simulator van te maken, kan je als volgt te werk gaan. Voeg deze code op de juiste plaats toe.

We definieren een array van buildings, die gekenmerkt worden door een punt (top) en de breedte. Deze array vullen we met willekeurige waarden.
Alle gebouwen worden getekend met rechthoeken, als hun positie positief is (tov het zichtspunt). Anders kan het programma al eens crashen...
Check of een building wordt geraakt.
The Flight Simulator (raak zo weinig mogelijk gebouwen, of net zoveel mogelijk...)

H1: FiguurTekenaar.

Gegeven zijn procedures om de volgende figuren te tekenen: cirkel, ellips, vierkant, ster en driehoek.
Maak een programma die figuren tekent door aan de gebruiker te vragen welke figuur hij wilt, met welke kleur en deze figuur dan op een willekeurige positie tekent met een willekeurige grootte.
Een procedure om een willekeurig getal te genereren is ook gegeven.

Copieer deze code en bestudeer de gegeven procedures.
Definieer een figuur-type met de volgende eigenschappen: figuurtype, middelpunt, grootte en kleur.
Vraag de gebruiker welke figuur hij wilt en met welke kleur, vul de waarde in een figuur-variabele.
Maak een TekenFiguur procedure die deze figuur tekent: een procedure die een figuur (zoals in punt 2 gedefinieerd) als input neemt.
Genereer dan random waarden voor middelpunt en grootte, en teken de figuur.
Zet bovenstaande in een lus: teken figuren tot de gebruiker 0 intikt voor de kleur.

H2: Zwaartepunt

Start with this code.
The type for a point is defines as:

TYPE PointRc = RECORD

x, y: REAL;

END;

Define the variable arr which can contain 10 points (punten) in a two-dimensional space, thus use the given type PointRc.
Make a procedure that plots an array of points, an array of arbitrary (willekeurige) size (use an open array!).

convert the coordinates to fit the graph screen: multiply them by a scale factor (use a constant for this).
draw a small square with size SIZE for every point.

Make a procedure that calculate the centre of gravity (zwaartepunt) cg and returns a record for this.

formula: cg = (sum xi/number, sum yi/number)
Print an asterisk (ster) in that point.

Calculate for each point the distance to the centre of gravity, add this to the datastructure! Print out all the 10 calculated distances.
Use this procedure that calculates the average distance of 1 point to an (open) array of points. Use this to calculate the average distance of the 10 points to the center of gravity. Draw a circle to indicate this average distance.
Mark the points that are further away from the calculated average distance to the centre of gravity. Add this property to the datastructure. Print this points in red.

T1: Output

What is the output of the following program?

MODULE T1;<* NOOPTIMIZE + *>
FROM IO IMPORT RdChar, WrChar, WrStr, RdStr, WrLn, RdCard, WrCard, RdInt, WrInt, RdReal, WrReal, RdBool, WrBool;

    CONST
       MIN = 2;
       MAX = 3;          (* constants *)

    TYPE Rc = RECORD
                 a, b: INTEGER;
              END;
         Ar = ARRAY[MIN..MAX] OF INTEGER;

    PROCEDURE Proc1(a, b, c: INTEGER): BOOLEAN;
      VAR toReturn: BOOLEAN;
    BEGIN
      a := a + b + 1;
      IF a > c THEN
        toReturn := TRUE;
      ELSE
        toReturn := FALSE;
      END;
      RETURN toReturn;
    END Proc1;

    PROCEDURE Proc2(a, b, c: INTEGER): INTEGER;
      VAR toReturn: INTEGER;
    BEGIN
      IF c > b THEN
        toReturn := (a + b) ;
      ELSE
        toReturn := (a + c) ;
      END;
      RETURN toReturn;
    END Proc2;

    PROCEDURE WrRc(c: Rc);
    BEGIN
      WrStr("field a = ");WrInt(c.a,0);WrLn;
      WrStr("field b = ");WrInt(c.b,0);WrLn;
    END WrRc;
    PROCEDURE WrAr(c: ARRAY OF INTEGER);
    (* procedure that prints the array *)
      VAR i: CARDINAL;
    BEGIN
      FOR i := 0 TO HIGH(c) DO
        WrStr("El ");WrCard(i,0);WrStr(" = ");WrInt(c[i],0);WrLn;
      END;
    END WrAr;

    VAR c:Rc;            (* variable-declarations *)
        d:Ar;
BEGIN
    WrLn;
    c.a := 1;
    c.b := 2;
    d[2] := 3;
    d[3] := 4;

    WHILE Proc1(c.b, d[2], c.a) DO
      c.a := Proc2(d[2], d[3], c.b);
      DEC( d[2]);   (* definition of Decrement: DEC(n); is similar as n := n - 1; *)
      DEC( d[3]);
    END;
    WrRc(c);
    WrAr(d);
END T1.